Abstract
First, a lame joke. Then, a brief and sketchy outline of signal detection. Then, some simulations of PET's abilities to differentiate between "no effect" and modal social psychology effects. Then, comparing the signal detection properties of PET to comparable methodological choices from individual experiments. Then probably a bunch of caveats. Maybe another bad joke, too. Or maybe some music.
tl;dr summary: Under some conditions, using PET in a meta-analysis makes as much sense as running an experiment with 7 participants.
go
Will Gervais, circa 1999
Back in high school and middle school, I spent a lot of time roaming around Summit County, CO on a BMX bike and skiing and snowboarding and whatnot. I tooled around in a VW Golf. I was moderately into punk rock. Bands like Rancid, Green Day, Lagwagon, and NOFX. Speaking of NOFX, I feel lately like my current professional life is circling back on my previous small town high school life in an odd way.
You see, NOFX had an album called Heavy Petting Zoo (witty, right?). And now in my professional life, I'm seeing a lot of people starting to heavily use a technique called PET to declare no evidence for various effects. Get it? Heavy PETting for No Effects? Okay, now that you've had time to clean up the coffee you spilled laughing at that hilarious (and waaaay forced) joke, it's time to move on.
I've previously blogged about PET. It's a new-ish tool designed with the intention of letting us get good estimates from meta-analyses in the presence of publication bias. Like many, I am enthusiastic about the development of tools like this. Also, like many, I'm becoming a bit disenchanted by the idea that we can slap a correction onto a meta-analysis of a heavily biased literature and hope to get a good answer. Hopefully, we'll find something that works. I don't think we're there yet. And PET, in particular, worries me.
Why PET worries me
PET is super easy to use. And it's cropping up more and more frequently in the published literature. In social psych, I informally count 13 published uses of PET, a handful of submitted versions, and I recently reviewed a paper using PET. In every single instance I've found, PET has returned an effect size estimate that doesn't differ from zero. And in every single instance, the authors interpret the result as some flavor of "there is therefore no evidence of this effect" or "the evidence for this effect is lacking/overstated/wonky." On the one hand, simulations show that PET is pretty good at estimating effects when none are present. More problematically, it also seems to frequently say that real effects are consistent with zero.
When it comes to questions like "is this effect real or not?" it isn't sufficient to have a tool that adequately describes nil effects as nil. We need tools that can also adequately describe real effects as real. Fundamentally, this is a signal detection problem: which tools are good at finding signals amongst noise? I don't think PET is that tool.
Signal detection theory
Signal detection theory is an approach for quantifying a process's abilities to differentiate signals from noise. Essentially, you can break it down into a 2 x 2 grid. A signal can be present or absent. The process makes a judgment about whether or not a signal is present. This results in four possible outcomes.
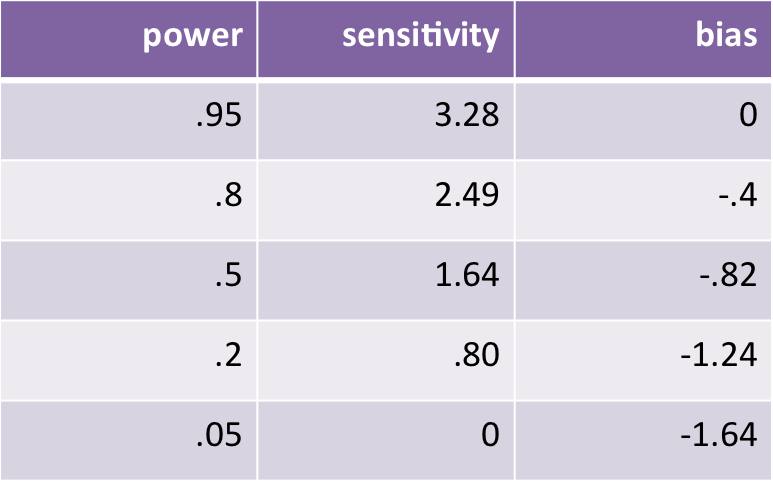
You can do some math to distill a couple of parameters by comparing rates of hits and false alarms. Sensitivity (d') is the process's ability to sift signal from noise. Bias (C) is the process's tendency to reply one way or another, regardless of the presence or absence of a signal. If you're like me, the d' and C values don't make much sense on their own. So with that in mind, here are the signal detection properties of a significance test with alpha set at .05 at varying levels of statistical power (with the dodgy assumption that our population of "signals" are an equal mix of real effects and nils).
Note: I flipped the sign from traditional signal detection bias calculations so that negative values refer to negative bias, or bias against "detecting" signals.
To unpack this, running studies with 95% power yields (unsurprisingly) good sensitivity: high-powered studies are good at finding signals! That's why we should use them! At this stage, the process is unbiased because we've set beta equal to our nominal alpha of .05. As power declines, the test becomes less sensitive (worse at finding signals), and also negatively biased (you're more and more likely to miss genuine signals). This culminates in this case at 5% power: totally insensitive to the presence or absence of signals, and violently negatively biased. Detected "signals" are just as likely to be noise as genuine signals. So, how does PET stack up in this framework?
Time for some sketchy simulations.
I decided to run some sketchy simulations to answer the following question:
Can PET differentiate between the nil (d=0) and the modal effect size in social psychology (d= .16)?
This means I simulated a bunch of meta-analyses using PET when d=0, and a bunch when d=.16. Then I plugged things into some signal detection calculations. Here are some of the basic quirks of the sketchy simulations.
- each individual study has a sample size modeled after empirical estimates
for my field - 90% publication bias. So 90% of the studies in each meta-analysis are chosen because they're significant in the "right" direction. The other 10% fall wherever they may (sketchy assumption #1, but it certainly looks like our literature)
- Each meta-analysis gets 16 studies to work with. Why 16? It's the median number of studies included in published PETs I can find* (sketchy assumption #2)
- Fully heterogenous effect sizes (sketchy assumption #3)
- Simulate 1000 metas like this for each of d=0 and d=.16
- "Hit" = the proportion of PET CIs excluding zero when d=.16
- "False alarm" = proportion of PET CIs excluding zero when d=0
some sketchy results
First, how do things look? Well, PET looks spectacular when d=0. Given the heavy publication bias I simulated, the average observed effect size is d= .50. But PET's average estimate is a spot-on d = -.01. This is why people like PET: give it a true nil, and that's what it estimates.
Now for the bad news, what happens with the modal social psych effect size? PET's average estimate is .05, with an average CI that's almost .6 wide. Negatively biased, and not at all precise. The CI is more likely to include zero (94%) than the true effect size (79%).
signal detecting PET
In signal detection terms, PET is atrocious in these simulations. The false positive rate is a legitimately superb ~5%. The hit rate is a sad-panda 6%. This yields sensitivity (d') of .07, and bias (C) of -1.59.
As d' and C don't make any intuitive sense to me, I tried to find experiment-level methodological choices with comparable sensitivity and bias. After some trial and error, it turns out that using PET to tell whether an effect is zero or typical of social psych has roughly the same signal detection properties as running studies with 5.8% power (d' = .073, C = -1.68).
5.8%.
This is like chasing a modal social psych effect size (d = .16) with fewer than 13 participants per condition in a 2-group design. Or chasing a median social psych effect size (d = .36) with 3.4 participants per condition.
So, if you wouldn't run a study on a median social psych magnitude effect with a mere 7 participants...maybe hold off on using PET to ask whether or not an effect is real.
Objections
O1: This isn't a fair test! 16 data points is far too few for a regression technique like PET!*
A1: Agreed, that is far too few, and we shouldn't be doing regressions on 16 data points, no matter whether those data points are k studies or n participants. Regression is just a powerful-but-dumb golem that doesn't know the difference between n and k. But I picked 16 because it really, truly is the median number of studies in the published PETs I could find. So half of the published uses of this technique had less than that.
O2: Wow, 90% publication bias is harsh!
A2: Yes, it is. But that's what the literature looks like. Naturally, good meta-analyses try to ease this pressure by finding unpublished studies. But in some other simulations we find that at 50% publication bias and 100 studies per meta, PET's sensitivity is still only .31. That's equivalent to running 7 participants per condition while chasing a d = .36. I still wouldn't do it.
O3: Man, Will, there are a lot of sketchy assumptions built in there.
A3: Guilty as charged. But you have to start somewhere.
O4: Wow, you really must hate PET to blog about it a few times. And you sure must be angry at the early adopters who started promoting it.
A4: Not at all! I really want something like PET to work, and I have genuine admiration for early adopters like Mike McCullough and Evan Carter. I'm even the weak link on a big simulation project with Evan and some other rock stars (Joe Hilgard and Felix Schönbrodt) where hopefully we can sort this shit out and give some tangible recommendations about bias correction techniques (spoiler: don't hold your breath). I just think that when we're taking a justifiably skeptical approach to literatures, we should be just as skeptical of the new tools we're wielding against the literatures. And with more than a dozen published PETs (and presumably more being submitted weekly) I think it's probably time to ask how well it works on our literature.
O5: Why did you redact a picture of yourself in high school?
A5: Because I looked like a jackass.
O6: Cool story, bro. Can I see your code?
A6: Sure. Here it is. Usual caveats apply: It's clunky. Annotations are probably sketchy. And I can pretty much guarantee some glitches in there. So take it, improve it, and (hopefully!) find some conditions under which PET works better than the vastly underpowered studies it's supposed to correct for.
O7: Does this mean we should believe in phenomena red-flagged by PET?
A7: Of course not. My argument is that--just like an experiment with 7 participants--being red-flagged by PET doesn't mean much of anything. Insensitive tools can't answer that question.